18. EKF Example

EKF Example

Let's look at another example of a vehicle taking measurements - this time, a quadrotor! This quadrotor is a bit simplified - it's motion is constrained to the y-axis. Therefore, it's state can be defined by the following vector,

\large x = \begin{bmatrix} \phi \\ \dot{y} \\ y \end{bmatrix}

that is: its roll angle, its velocity, and its position.

Imagine you have a quadrotor, such as the one in the image below. This quadrotor would like to know the distance between it and the wall. This is an important measurement to have if the quadrotor would like to traverse the inside of a room, or outside of a building, while maintaining a safe distance from the wall.

To estimate this distance, the quadrotor is equipped with a range finger.

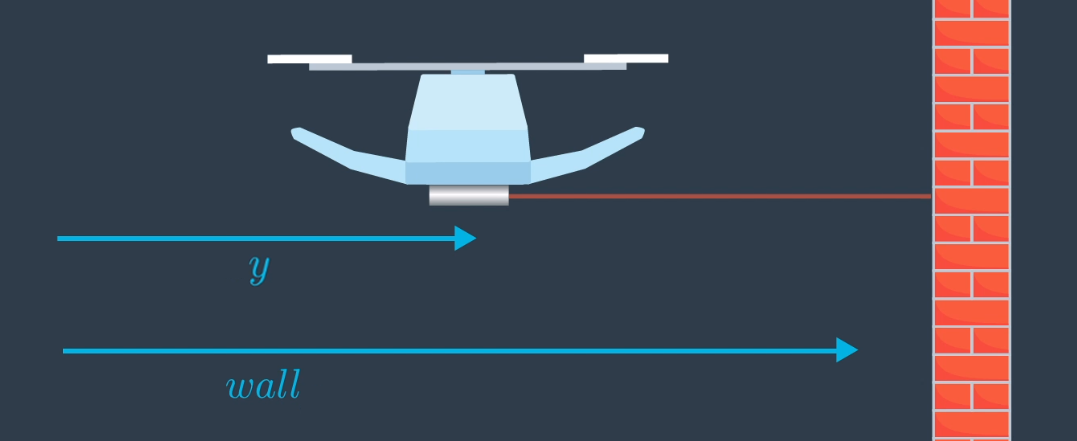
Shown in blue, are the true distances from an arbitrary point on the left to the quadrotor, and to the wall.

In the quadrotor's current configuration, what would you expect it's measurement to the wall to be?

SOLUTION:
h(x) = wall - y

That's right - while the quadrotor is hovering perpendicular to the wall, the measurement, h(x) , is equal to wall - y .

Now, what would happen if the quadrotor were to roll to some angle \phi ? What is a more general equation for the measurement that takes into account the roll angle?

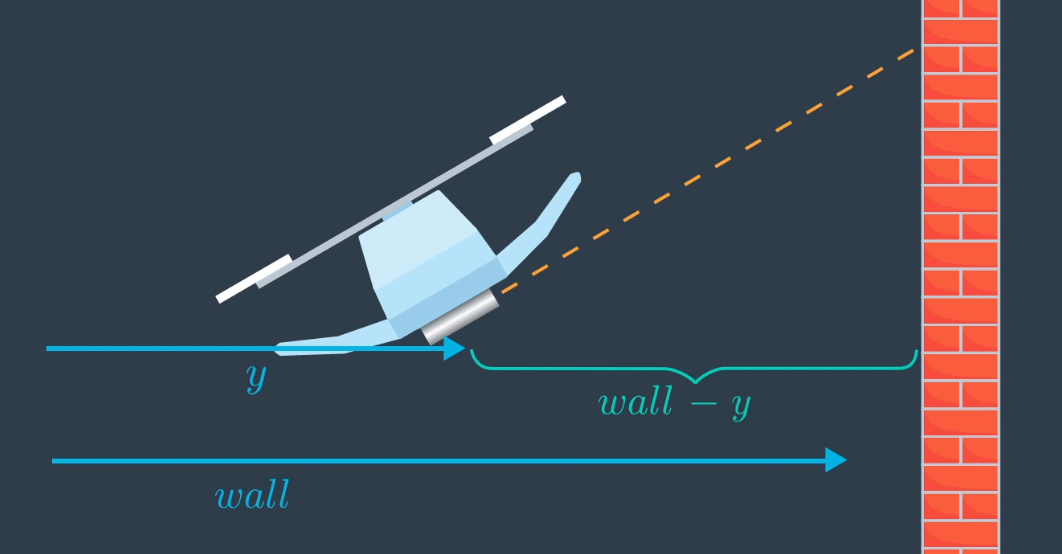
What is the equation for the measurement when the quadrotor has a roll angle of \phi ?

SOLUTION:
h(x) = \frac{wall - y}{cos \phi}

Applying some basic trigonometry, we've now determined the measurement model for this quadrotor's range finder.

\large h(x) = \begin{bmatrix} \frac{wall - y}{cos \phi} \end{bmatrix}

The function has a cosine in it's denominator, making this function non-linear. This means that we will need to use the Extended Kalman Filter for our estimation, and in the process, linearize the function.

Calculating H

To apply the Extended Kalman Filter, we will need to calculate H, the Jacobian of the measurement model that we defined above. This won't be too strenuous since the measurement function is a 1x1 matrix.

Without calculating the partial derivatives, which of the following is the correct Jacobian for the measurement model?

Select the correct Jacobian for the measurement model.

SOLUTION:
\large H = \begin{bmatrix} \frac{\delta h}{\delta \phi} & \frac{\delta h}{\delta \dot{y}} & \frac{\delta h}{\delta y} \end{bmatrix}

Calculating the three partial derivatives will result in the following,

\begin{aligned} \frac{\delta h}{\delta \phi} &= \frac{sin \phi}{cos^2 \phi} (wall - y) \\ \frac{\delta h}{\delta \dot{y}} &= 0 \\ \frac{\delta h}{\delta y} &= \frac{-1}{cos \phi} \end{aligned}

When implementing the Extended Kalman Filter in code, there are software libraries that can take the partial derivative of a function, simplifying your implementation. There are, of course, also EKF implementations readily available too. However, it's always helpful to understand the inner workings of an algorithm and apply it intelligently to the problem at hand.

After calculating H,

\large H = \begin{bmatrix} \frac{sin \phi}{cos^2 \phi} (wall - y) & 0 & \frac{-1}{cos \phi}\end{bmatrix}

it can be used in the EKF equations to update the covariance of the state.

As a reminder, the equations are provided below:

Extended Kalman Filter Equations

The matrices in blue display where the Jacobian is used, if the underlying state transition or measurement function is nonlinear.

State Prediction:

\large \color{black} x' = f(x)
\large \color{black} P' = \color{blue}F\color{black}P\color{blue}F^T\color{black} + Q

Measurement Update:

\large \color{black} y = z -h(x')
\large \color{black} S = \color{blue}H\color{black}P' \color{blue}H^T\color{black} + R

Calculation of Kalman Gain:

\large \color{black} K = P' \color{blue}H^T\color{black}S^{-1}

Calculation of Posterior State and Covariance:

\large \color{black} x = x' + Ky
\large \color{black} P = (I - K \color{blue}H\color{black})P'

Next Concept